| Mathematische Zeichen |
| Griechische Buchstaben |
| Maßeinheiten |
| Übungsbeispiele: Flächen und Volumsberechnungen |

|
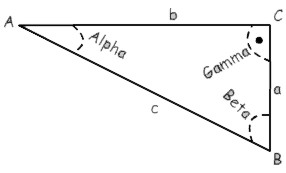
a = g - b a = INV tan a / b |
b = g - a |
g = a + b |
c = a / sina c = Ö(a² + b²) |
a = c * sina a = Ö(c² - b²) a = b * tana |
b = Ö(c²- a²) |
|
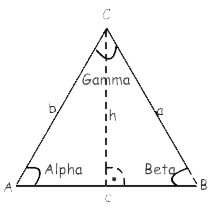
u = 3 * a |
A = a²/ 4 *Ö3 |
h = a/ 2 *Ö3 |
a = u / 3 a = Ö((A * 4) / Ö3) a = (h * 2) / Ö3 a = b = c!! |
|
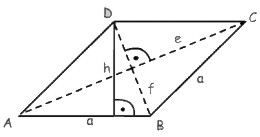
u = 4 * a |
A = (e * f) / 2 A = a * h |
h = A / a |
e = Ö( 2a² - f²) e = (A * 2) / f |
a = u / 4 a = Ö((e² / 2) + (f² / 2)) a = A / h |
|
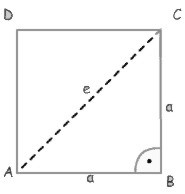
u = 4 * a
|
A = a²
|
e = a * Ö 2 |
a = e / Ö2 a = ÖA a = u / 4 |

|
A = a * b
|
u = 2a + 2b
|
e = Ö (a² * b²) |
a = A / b a = (u - 2b) / 2 a = Ö (e² - b²) |
b = A / a b = (u - 2a) / 2 b = Ö (e² - a²) |
|
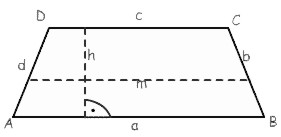
a = u - b - c - d a = m * 2 - c |
b = u - a - c - d b = u - m * 2 - d |
c = u - a - b - d c = m * 2 - a |
d = u - a - b - c d = u - m * 2 - b |
|
m = (a + c) / 2 m = a / h m = (u - b - d) / 2 |
u = a + b + c + d
u = m * 2 + b + d |
h = a / m h = a / ((a + c) / 2) |
A = m * h A = ((a + c) / 2) * h |

|
A = a * h A = b * h |
u = 2 * (a + b ) |
h= A / b |
h= A / a |
b = U / 2 - a b = A / h |
a = U / 2 - b a = A / h |
|
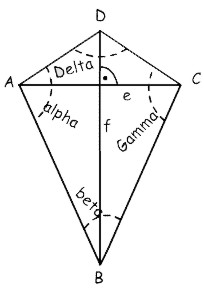
a = (u / 2) -b |
b = (u / 2) - a |
e = (A * 2) / f |
A = (e * f) / 2 |
f = (A * 2) / e f =Öa² - (e / 2)² + Öb² - (e / 2)² |
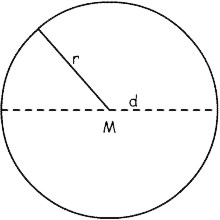
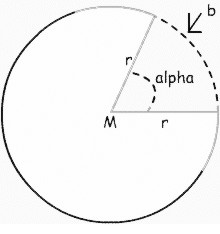
| u = 2 * p * r | A = p * r² | d = 2 * r |
r = d / 2 r = Ö(A / p) r = u / (2 * p) |
|
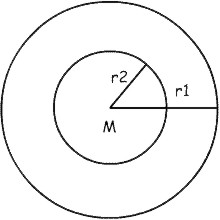
A = p * (r² - r²) |
u = 2 * p * (r- r) |
r= Ö ((A / p) + r²) r= u / ( 2 * p) - r |
r= Ö ((A / p) + r²) r= U / ( 2 * p) - r |
|
a = (A * 360) / (p * r²) |
A = (b * r) / 2 |
b = (A * 2) / r b = 2 * p * r * a / 360 |
r = (A * 2) / b r =Ö(A * 360) / (p * a) r = (b * 360) / (a * 2 * p) |
|
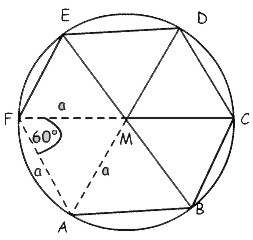
u = 6 * a |
A = 3 / 2 * a² * Ö3 A = 6 * (a² / 4 * Ö3) |
h = a / 2 * Ö3 |
a = h * 2 / Ö3 a = Ö((a / 6) * 4) / Ö3 a = u / 6 |
|
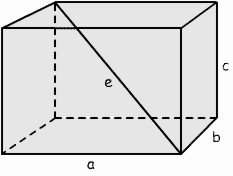
O = 2 (a * b + b * c + a * c) |
V = a * b * c |
b = ((O / 2) - a * c) / ( a + c) b = V / (c * a) b = Ö(e² - c² - a²) |
|
c = ((O / 2) - a * b) / ( a + b) c = V / (b * a) c = Ö(e² - a² - b²) |
e = Ö(a² + b² + c²) |
a = ((O / 2) - b * c) / ( b + c) a = V / (c * b) a = Ö(e² - b² - c²) |

|
4 |
V = a³ |
e = a * Ö3 |
a = Ö(O / 6) a = e / Ö3 a = ³ÖV = V hoch 1/3 |
|
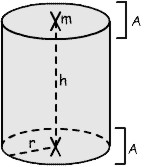
A = r² * p A = (O - M) / 2 |
V = p * r² * h |
O = 2 * p * r *(r + h) O = M + 2 * A |
|
M = O - (2 * A) |
r = Ö(V / (h * p)) r = Ö(A / p) r = Ö(( O - M) / (2 * p)) |
h = (O / (2 * r * p)) - r h = V / (r² * p) |
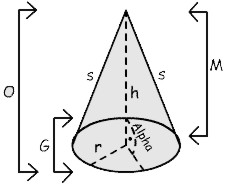
|
a = (r / s) * 360 |
h = Ö(s² - r²) |
h = Ö(s² - r²) h = V / ((p / 3) * r²) |
O = p * r² + p * r * s |
|
G = O - M G = p * r² |
s = M / (p * r) s = (r * 360) / a s = Ö(r² + h²) s = (r / a) * 360 |
r = Ö(G / p) r = ÖV / (h * (p / 3)) r = (a / s) / 360 r = Ö(s² - h²) r = -(s / 2) + Ö((s / 2) + (O / p)) |
V= (p / 3) * r² * h |
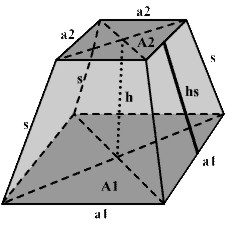
|
a =Ö ((3*V) / h) a = 2Ö (hs ²- h²) a = 2Ö (s² - hs²) a =(M / hs) / 2 a =ÖG a =Ö(O - M) |
h = (V * 43) / a² h = Ö (hs² - (a / 2)²) |
hs = M / ( 2 * a ) hs = Ö (h² + ( a / 2 )²) hs = Ö (s² - (a / 2 )²) hs = (O - a²) / 2a |
O =a² + 2a * hs O = G + M |
|
G = a² G = O - M |
s = Ö (hs² +( a / 2)²) |
V= (1/3) * a² * h V = (1 / 3) * G * h |
|
a = Grundkante; h = Höhe über dem Mittelpunkt; hs = Seitenhöhe; O = Oberfläche
M= Mantel ( 4 Dreieck); G = Grundfläche; V = Volumen; s = Seitenkantenlänge;
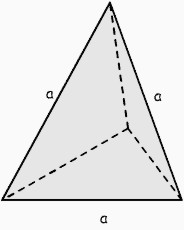
|
O = a² * Ö3 |
V = (a³ / 12) * Ö2 |
a = Ö(O / Ö3) a = ³Ö( (V * 12) / Ö2) |
d = u - a - b - c d = u - m * 2 - b |

|
s =Ö (h² + ( r1 - r2)²) s = M /(p *( r1 +r2)) |
A1 = p * r 1² A2 = p * r2² |
O = p * (r1²+r2²) + p * s * (r1 + r2) O = M + A1 +A2 |
|
M = p * s *(r1 + r2) |
r1 = (Ö(s² - h²)) + r2 r1 = (M / ( p * s)) - r2 r1 = Ö (A1 / p) |
h = (V * 3) / ( p *(r1² + r1 * r2 + r2²) h = Ö(s² - (r1 - r2)²) |
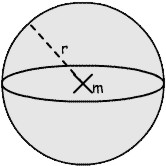
|
O = 4 * p * r² |
V = (4 / 3) * p * r³ |
d = 2 * r |
r = d / 2 r = Ö(O / (4 * p)) r = ³Ö( V / (4 / 3 * p)) |
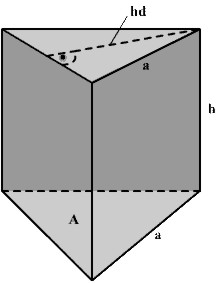
|
M = U * h M = 3 * a * h M = O - 2 * A |
O = M + 2 * A O = 3ah + (2 * a² * Ö3) / 4 O = a ( 3h + ((aÖ3) / 2)) |
h = ( V * 4) / (a² * Ö3) h = M / U h = M / ( 3 * a) h = V / A h = (( O / a) - ((aÖ3) / 2) ) / 3 |
a = U / 3 a = (2 * hd) / Ö3 a = Ö (4 * (A / Ö3)) a = Ö (( 4 * V) / (Ö3 * h)) a = M / ( 3* h) |
|
U = 3 * a |
hd = (a / 2) * Ö3 |
A = ( a² / 4) * Ö3 A = ( O - M) / 2 A = V / h |
V = A * h V = (( a² * h) / 4) * Ö3 |
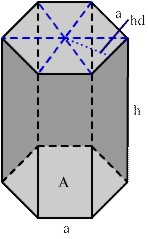
|
hd = (a / 2) *Ö3 |
U = 6 * a |
h = V / A h = M / U h = M / ( 6 * a) h = ( V * 2) / ( Ö3 * 3a²) h = ((O / (3a)) - aÖ3) / 2 |
a = ( hd *2) / Ö3 a = Ö(((A / 6) * 4) / Ö3) a = U / 6 a = M / ( 6 * h) a = Ö( ( V * 2) / (Ö3 * 3 * h) ) |
|
V = A * h V = ((3a² * h) / 2) * Ö3 |
M = 6 * a * h M = U * h M = O - 2A
|
A = (3a² / 2) * Ö3 A = 6 * (a² / 4) * Ö3 A = V / h A = O - M / 2 |
O = M + 2 * A O = 6 * a * h + ((2 * 3a² * Ö3) / 2) O = 3 * a * (2h + aÖ3) |
Der quadratische Pyramidenstumpf

|
h = (V / ( a1² + a1 * a2 + a2²)) * 3 h = Ö(s² - ((a1 - a2)² / 2)) h = Ö(hs² - ((a1 - a2)² / 4)) |
a2 = ÖA2 a2 = (Ö(2*(s² - h²)) - a1) * -1 a2 = (Ö(4 * (s² - hs²)) - a1) * -1 a2 = (Ö(4 * (hs² - h²)) - a1) * -1 a2 = M / (2 * hs) - a1 |
M = O - A1 - A2 M = 2 * hs * (a1 + a2) |
|
V = ( h / 3) * (a1² + a1 * a2 + a2²) |
s = Ö(h² + ((a1 - a2)² / 2)) s = Ö(hs² + ((a1 - a2)² / 4)) |
hs = Ö(h² +((a1 - a2)² / 4)) hs = (M / (a1 + a2)) / 2 hs = Ö(s² - ((a1 -a2)² / 4 )) hs = (( O - a1² - a2²) / (a1 + a2)) / 2 |
|
a1 = Ö(4 * (hs² - h²)) + a2 a1 = Ö A1 a1 = Ö(2 * (s² - h²)) + a2 a1 = Ö( 4 * (s² - hs²)) + a2 a1 = M / (2 * hs) - a2 |
O = a1² + a2² + 2 * hs * (a1 + a2) O = M + A1 + A2 |
A1 = a1² A1 = O - M - A2 |
|
|
|
A2 = a2² A2 = O - M - A1 |
Der regelm. dreieckige Pyramidenstumpf
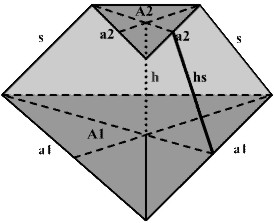
|
h = ((V / ( a1² + a1 * a2 + a2²)) * 12 / Ö3) h = Ö(s² - ((a1 - a2)² / 3)) h = Ö(hs² - ((a1 - a2)² / 12)) |
a2 = Ö(A2 * 4 / Ö3) a2 = (Ö(3*(s² - h²)) - a1) * -1 a2 = (Ö(4 * (s² - hs²)) - a1) * -1 a2 = (Ö(12 * (hs² - h²)) - a1) * -1 a2 = (2 * M) / (3 * hs) - a1 |
|
V = ( h * Ö 3 / 12) * (a1² + a1 * a2 + a2²) |
s = Ö(h² + ((a1 - a2)² / 3)) s = Ö(hs² + ((a1 - a2)² / 4)) |
|
O = ((a1² + a2²)* Ö3) / 4 + (3 * hs * (a1 + a2) / 2) O = M + A1 + A2 |
a1 = Ö(12 * (hs² - h²)) + a2 a1 = Ö(A1 * 4 / Ö3) a1 = Ö(3 * (s² - h²)) + a2 a1 = Ö( 4 * (s² - hs²)) + a2 a1 = (2 * M) / (3 * hs) - a2 |
|
hs = Ö(h² +((a1 - a2)² / 12)) hs = ((2 * M) / (a1 + a2)) / 3 hs = Ö(s² - ((a1 -a2)² / 4 )) hs = (( O - (((a1² + a2²) * Ö3) / 4)) / ((a1 + a2) / 2)) / 3 |
|
Der regelm. sechseckige Pyramidenstumpf
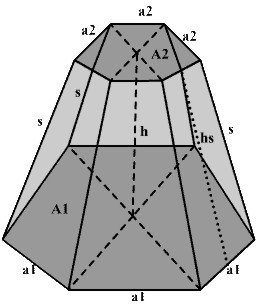
|
h =(( V / (a1² + a1 * a2 + a2²)) * 2 / Ö3) h = Ö(s² - (a1 - a2)²) h = Ö(hs² - (( 3 * (a1 - a2)²) / 4)) |
a2 = Ö(A2 / ( 3 / 2 * Ö3)) a2 = M / (3 *hs) - a1 a2 = (Ö(s² - h²) - a1) * -1 a2 = (Ö( 4 * (s² - hs²)) - a1) * -1 a2 = (Ö((hs² - h²) * 4 / 3) - a1) * -1 |
|
V = (( h * Ö 3) / 2) * (a1² + a1 * a2 + a2²)
|
s = Ö(h² + (a1 - a2)²) s = Ö(hs² + ((a1 - a2)² / 4)) |
|
O = ((3 * Ö3) / 2) * (a1² + a2²) + 3 * hs * (a1 + a2) O = M + A1 + A2 |
a1 = Ö(A1 / ( 3 / 2 * Ö3)) a1 = M / (3 *hs) - a2 a1 = Ö(s² - h²) + a2 a1 = Ö( 4 * (s² - hs²)) + a2 a1 = (Ö((hs² - h²) * 4 / 3)) + a2 |
|
hs = Ö(h² + ((3 * (a1 - a2)²) / 4)) hs = Ö(s² - ((a1 -a2)² / 4 )) hs = (M / 3) / ( a1 + a2) hs = ( O -3 * Ö(3) / 2 * (a1² + a2²)) / 3 / (a1 + a2) |
|
|
= |
gleich |
|
Winkel |
|
< |
kleiner als |
|
rechter Winkel(90°) |
|
> |
größer als |
|
Natürliche Zahlen ohne Null |
|
< |
kleiner oder gleich |
|
Ganze Zahlen |
|
> |
größer oder gleich |
|
Natürliche Zahlen |
|
» |
ungefähr gleich, rund |
AB |
Gerade durch A u. B |
|
Ù
|
entspricht |
__ |
Strecke zwischen A u. B |
|
¥ |
unendlich |
|
Rationale Zahlen |
|
|| |
parallel |
|
Reelle Zahlen |
|
^ |
rechtwinklig, senkrecht zu |
@ |
kongurent |
|
~ |
proportional, ähnlich |
‡ |
ungleich |
|
|
|
|
|
|
a |
Alpha |
o |
Omikron |
|
b |
Beta |
p |
Pi |
|
g |
Gamma |
t |
Tau |
|
d |
Delta |
u |
Ypsilon |
|
e |
Epsilon |
w |
Omega |
|
z |
Zeta |
x |
Xi |
|
h |
Eta |
y |
Psi |
|
l |
Lambda |
m |
My |
|
i |
Jota |
j |
Phi |
|
Zeitmaße = |
1 Jahr =
365 Tage
|
|
Gewichtsmaße = |
1 Mt =
1000 kt |
|
Längenmaße = |
1 km
= 1000 m
1 m = 10 dm 1 dm = 10 cm 1 cm = 10 mm |
|
Flächenmaße = |
1 km² = 100 ha
|
|
Raummaße = |
1 m³
= 1000 dm³
1 dm³ = 1000 cm³ 1 cm³ = 1000 mm³ |
|
Hohlmaße = |
1 hl
= 100 l 1 l = 1000 ml 1 dm³ = 1 l 1 ml = 1 cm³ |
Übungsbeispiele - Volumsberechnungen
Copyright © 2005 Hojager, Gerhard J. Hojas, Linz/Ebelsberg. Alle Rechte vorbehalten.